题目:输入某二叉树的前序遍历和中序遍历的结果。请重建出该二叉树。如果输入的前序遍历和中序遍历的结果中都不含反复的数字。
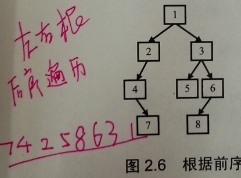
比如:输入前序遍历 {1,2,4,7,3,5,6,8} 和中序遍历序列 {4,7,2,1,5,3,8,6},则重建出图2.6所看到的的二叉树并输出它的头结点。
感触:复杂问题,要将它分解成一个个小问题,逐个击破,从而解决大问题。
我们都知道一个概念。知道 前序遍历 和 中序遍历。能够唯一确定一颗二叉树。
因此,我们首先须要怎样依据这两个已知条件,来画出这颗二叉树。在解决这道题的时候,最好用纸和笔。自己先实现一遍,然后分析自己实现的过程。分解每个步骤,而问题的算法就是依据你解决这个问题的步骤而来。
我在做的过程中,曾參考书中代码,然而别人的代码终究不是自己的。是别人的思路,自己在理解的过程中,总有这样那样的问题。因此。最好将书上的代码放一边,自己动手
去实践。依照自己的思路来解决整个问题。这样你在測试的时候。才有针对性。当然对于书中代码呈现的解决思路,须要选择性吸收。
对于这个问题,我把它分成三步:
1、首先拿到前序遍历序列,其作用就是用来取得 根节点。
(须要理解,二叉树是一个递归的过程,其子树亦是一个二叉树。每一次都是取得 二叉树的根节点)
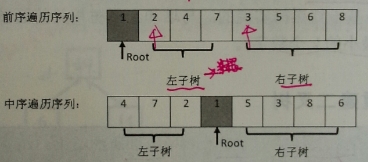
2、找到 “前序遍历中取得的根节点” 在中序遍历序列中的位置
3、找到该位置后,就能够确定 该根节点 所接的左右子树(例如以下图所看到的),然后对这 子 二叉树进行递归操作。
这样又从第一步開始了。依次取得每一棵子二叉树的根节点。从而完毕整棵树的重建。
代码例如以下:
在解决这个问题的过程中,常常出现考虑问题不全面的问题,比方 以下代码中,加的一个函数 Judge_array()。它用来測试当你输入的前序序列和中序序列 不匹配的情况。这一点一開始乜有考虑到。
须要 铭记。警醒!
剑指offer中。有句话说的非常好,“最好在写代码前,考虑好測试用例“。在撸代码的过程中,特别有感触。
/****************************************************************************//** 题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。 *//** 如果输入的前序遍历和中序遍历的结果中都不含反复的数字。比如 *//** 输入前序遍历{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6} *//** 则重建出图2.6所看到的的二叉树并输出它的头结点。 */ /** 时间:2015.7.25 作者:jwt */ /****************************************************************************/ #include <iostream> using namespace std; typedef struct node { int value; struct node *lchild; struct node *rchild; }BiTree_Node; /**用于推断前序遍历序列和中序遍历数列书否匹配*/ bool Judge_array(int *pre,int *in,int n) { int i, j; int k = 0; for(i = 0; i < n; i++) { for(j = 0; j < n; j++) { if(pre[i] == in[j]) k++; } } if(k != n) return false; else return true; } /*重建二叉树的递归操作,对于这个问题。用指针更加方便 */ BiTree_Node *Construct(int *pre_start, int *in_start, int len) { /**对于前序遍历数列,仅仅做一件事,取得根节点root */ int root_value = pre_start[0]; BiTree_Node *root; root = new BiTree_Node; root->value = root_value; root->lchild = NULL; root->rchild = NULL; /**在中序遍历中寻找上面取得的root的位置*/ int k = 0; int new_len; while(root_value != in_start[k] && k < len) { k++; } new_len = k; /**依据所找到的位置,推断左右子树*/ if(new_len > 0) { root->lchild = Construct(pre_start+1, in_start, new_len); /*new_len 表示左子树的长度*/ } if(len - new_len - 1> 0) { root->rchild = Construct(pre_start+new_len+1, in_start+new_len+1, len-new_len-1); /*len-new_len-1 表示右子树的长度*/ } return root; } /*重建二叉树函数*/ BiTree_Node *Construct_BiTree(int pre[],int in[],int length) { if(pre == NULL || in == NULL || length <= 0 || !Judge_array(pre, in, length)) return NULL; else return Construct(pre, in, length); } /**二叉树后序遍历。通过后序遍历推断重建的二叉树是否正确*/ void Postorder(BiTree_Node *root) { if(NULL == root) return; else{ Postorder(root->lchild); Postorder(root->rchild); cout << root->value << ' '; } } int main() { int pre[8] = {1,2,4,7,3,5,6,8}; int in[8] = {4,7,2,1,5,3,8,6}; //int pre[5] = {1,2,3,4,5}; //int in[5] = {5,4,3,2,1}; //int pre[6] = {1,2,3,6,7,8}; //int in[6] = {3,2,1,6,7,8}; //int pre[5] = {1,2,3,4,5}; //int in[5] = {1,2,3,4,6}; BiTree_Node *root = Construct_BiTree(pre,in,8); Postorder(root); return 0; }
结果例如以下:(能够用主函数凝视部分。測试其它情况)
/*点滴积累,我的一小步O(∩_∩)O~*/